[09] 이산수학(행렬을 이용한 연산)

주대각선 : 파란색으로 표시된 부분의 성분은 행렬 A의 주대각선 상에 있다.

대각합 :

• 주대각선 위 모든 성분들을 대각항이라 하고, 대각항들의 합을 대각합이라고 한다.
• 정방행렬 A의 대각합은 tr(A) 또는 trace(A)로 표기한다.
• 행렬의 대각합은 행과 열 번호가 같은 성분들의 합과 같다.

 

영행렬(Zero matrix) : 

• 성분이 모두 0인 행렬
• 모든 i,j에 대하여 a(ij) = 0인 행렬을 말하며, 간단히 볼드체의 O이라고 표기한다.

교대 행렬(Skewed-symmetric matrix) :

• 전치행렬에 (-)를 붙인 n x n 행렬을 교대행렬이라고 한다.

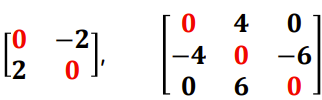
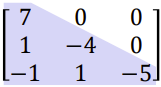
삼각 행렬(Triangular matrix) : 

• 상부삼각행렬(upper triangular matrix) : 주대각선 아래에 있는 모든 항들이 0인 n x n인 행렬

• 하부삼각행렬(lower triangular matrix) : 주대각선 위에 있는 모든 항들이 0인 n x n인 행렬

---

행렬의 기본 연산 : 

기본 행 연산(elementary row operation) :

• Type 1 : 어떤 2개의 행을 서로 바꾼다.
• Type 2 : 어떤 행에다 0이 아닌 상수를 곱한다.
• Type 3 : 어떤 행에다 상수를 곱한 후 다른 행에다 더한다.

행 사다리꼴(REF, Row Echelon Form) :

• 피벗(pivot) 또는 선행자(leading one) : 사다리꼴 행렬의 각 행에서 0이 아닌 가장 처음 나타나는 수
• m x n 행렬 A가 기본 행 연산들을 거친 후 다음 3가지 조건을 만족하면 행 사다리꼴이라 한다.
  1. 0으로만 이루어진 행들이 존재한다면 행렬의 아래쪽에 나타난다.
  2. 모두가 0이 아닌 행의 가장 왼쪽에 처음 나타나는 0이 아닌 수를 피벗으로 삼는다.
  3. 모두가 0이 아닌 두 행이 연달아 있으면 아래쪽 행의 피벗은 위쪽 행의 피벗보다 오른쪽에 있다.
• 위의 조건에 추가로 다음 조건까지 만족하면 기약 행 사다리꼴(RREF, Reduced REF)이라 한다.
  1. 한 행의 피벗을 포함하는 열(column)에는 피벗 이외의 항들은 모두 0이다.

행 사다리꼴을 기약 행 사다리꼴로 바꾸는 방법 :

• 기본 행 연산 순서 : 
  1. 전항 단계 : 피벗 아랫부분이 0이 되도록 만든다.
  2. 후항 단계 : 피벗의 윗부분까지 0이 되도록 행 연산을 수행한다.
• 가우스 소거법(Gauss elimination) :
  • 전항단계까지의 연산 과정을 수행하여 행 사다리꼴을 구하는 소거법
• 가우스 - 조단 소거법(Gauss - Jordan elimination) :
  • 후항단계까지 수행하는 소거법
• 계수(rank) :
  • 주어진 행렬을 행 사다리꼴로 만들었을 때, 행 전체가 0이 아닌 행의 개수

---

행렬식 :

• 정방행렬 A에 하나의 스칼라 값을 대응시키는 함수로서 Det(A) 또는|A|로 표시한다.

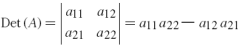
• 특이행렬 : n x n 정방행렬 A의 행렬식 |A|의 값이 0이 아닐 때 정칙행렬이라 하고 0일 때 특이행렬(singular matrix)이라 한다.
• 두 개의 행(또는 열)을 교환한 행렬식은 원래 행렬식에서 부호만 바뀐다.
• Det(AB) = Det(A) * Det(B)
• 행렬식의 어떤 행(또는 열)의 각 원소에 같은 수 k를 곱하여 얻은 행렬식은 처음 행렬식에 k를 곱한 것과 같다.
• n x n 행렬 A의 한 행(열)에 있는 모든 원소가 0이면 Det(A) = 0이다.

소행렬과 소행렬식 : 

소행렬 : 

• n차 정사각행렬에서 i번째 행과 j번째 열을 제거해서 얻은 (n-1) x (n-1)행렬

소행렬식 : 

• n차 정사각행렬의 소행렬 M(ij)에 대한 소행렬식

 

여인수와 여인수행렬 : 

• 계수를 여인수, 그 계수들로 이루어진 것을 여인수행렬이라 한다.

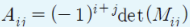
n차 정사각행렬 A에 대한 행렬식은 다음과 같다.

---

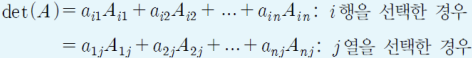
역행렬 : 

• 스칼라 값에서의 곱셈에 대한 역원과 유사한 개념으로 선형방정식의 풀이에서 매우 중요한 역할이다.

• 가우스 - 조단 방식 : 

역행렬을 이용한 선형방정식의 해 구하기 : 

연립방정식이 다음과 같을 때,

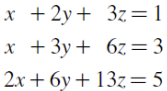
행렬로 표현하는 다음과 같고,

이를 이용하여 역행렬을 구하여 구한 답은

이다.

 

가우스 소거법 : 

• 상부사각행렬 후
• 후진대입법