[06] 이산수학(집합)

주제 : 집합

---

집합의 표현법 :

• 원소나열법 : 집합의 원소를 모두 나열하는 것
• 조건 제시법 : 집합의 원소들의 공통적인 특성을 기술하는 것

집합의 구간 : 닫힌구간, 열린 구간

두 집합이 같은 원소를 갖고 있다면 그 두 집합은 같다고 표현한다.

 

특수한 집합 :

• 공집합 : 원소를 갖지 않는 특수한 집합
• 단일 원소 집합 : 단 하나의 원소만 갖는 집합{공집합}

벤 다이어그램 : 집합 간의 관계를 나타내는 데 종종 사용한다

부분집합 : 임의의 집합 S에 대해 포함되는 원소들의 집합

진부분집합 : 공집합과 자기 자신을 제외한 부분집합

멱집합 : 임의의 집합 S가 주어졌을 때, 집합 S의 멱집합은 집합 S의 모든 부분집합의 집합이다.

 

데카르트곱 : 집합은 원소의 순서를 무시하지만, 여기서는 순서를 고려한다고 가정한다.

(두 순서쌍 (a, b)와 (c, d)는 a=c, b=d일 때 서로 같다고 한다.

관계 : 데카르트 곱 AxB의 부분집합 R을 집합 A로부터 집합 B로의 관계라고 한다.

 

진리 집합 : 술어 P와 정의역 D가 주어졌을 때 P(x)를 참으로 만드는 원소들의 집합이다.

(정의역 U가 주어졌을 때 ∀xP(x)는 P의 진리 집합이 정의역 U와 같을 때 참이다.)

 

합집합 : 집합 A 또는 B에 속하거나 양쪽에 모두 속하는 원소들을 포함하는 집합이다.

교집합 : 집합 A와 B 양쪽에 모두 속한 원소들을 포함하는 집합이다.

두 집합의 교집합이 공집합일 때 두 집합은 서로소라고 한다.

그 외 : 차집합, 대칭 차집합, 여집합

 

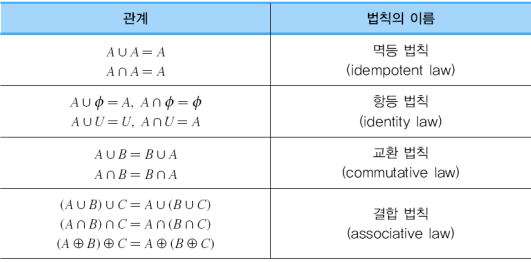
집합의 대수법칙 : 멱등 법칙, 항등 법칙, 교환 법칙, 결합 법칙, 분배 법칙, 흡수 법칙, 보 법칙, 역 법칙, 드 모르간의 법칙

중복집합은 참고만 하자.

중복집합 : 원소가 한 번 이상 나타나는 원소들의 순서 없는 모임